[NOIP2002 普及组] 过河卒

题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0, 0)$、$B$ 点 $(n, m)$，同样马的位置坐标是需要给出的。

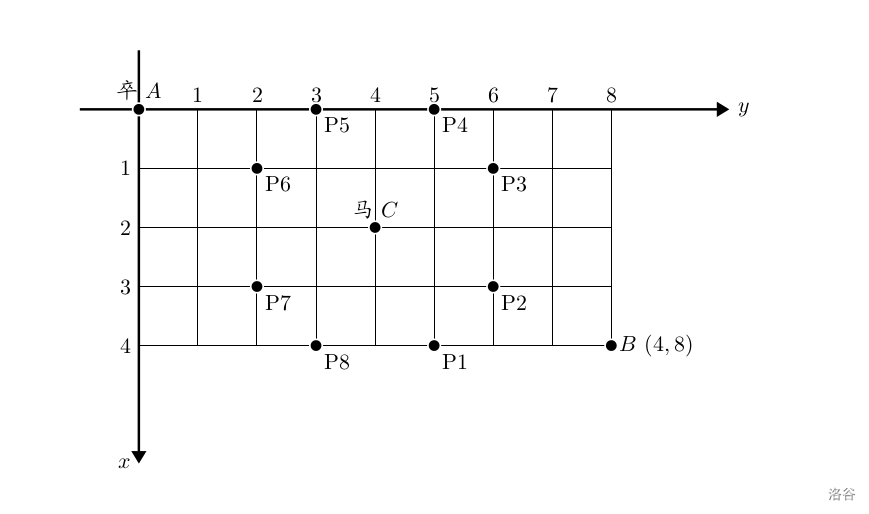
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例 #1

样例输入 #1

6 6 3 3

样例输出 #1

6

提示

对于 $100 %$ 的数据，$1 \le n, m \le 20$，$0 \le$ 马的坐标 $\le 20$。

【题目来源】

NOIP 2002 普及组第四题

分析得知可以按照递推的方式向后做，因为没有向前的可以影响的。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <cmath>
#include <cstdlib>
#include <queue>
#define LL long long
#define endl "\n"
#define int long long
#define rg register
#define pli pair<LL,int>
#define pil pair<int,LL>
#define debug(x) std:: cout << "---DEBUG--- " << x << " -----DEBUG----\n"
#define rep(a,b,c) for(int i = a; i < b; i += c)
#define repr(a,b,c) for(int i = a; i > b; i -= c)

using namespace std;
int dp[50][59];
signed main() {


    int n, m;
    int a, b;
    cin >> n >> m;
    cin >> a >> b;
    n++,m++,a++,b++;
    int x[10], y[10];
    x[1]=a-1;
    y[1]=b-2;
    x[2]=a-2;
    y[2]=b-1;
    x[3]=a+1;
    y[3]=b-2;
    x[4]=a+2;
    y[4]=b-1;
    x[5]=a-1;
    y[5]=b+2;
    x[6]=a-2;
    y[6]=b+1;
    x[7]=a+1;
    y[7]=b+2;
    x[8]=a+2;
    y[8]=b+1;
    x[9]=a;
    y[9]=b;
    dp[1][1]=1;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            int flag = 1;
            for(int k = 1; k <= 9; k++){
                if(x[k] == i && y[k] == j) flag = 0;
            }
            if(flag == 0) continue;
            dp[i][j] += dp[i][j-1] + dp[i-1][j];
        }
    }
    cout << dp[n][m];



    return 0;
}