图书整理

读者来到图书馆排队借还书，图书管理员使用两个书车来完成整理借还书的任务。书车中的书从下往上叠加存放，图书管理员每次只能拿取书车顶部的书。排队的读者会有两种操作：

push(bookID)：把借阅的书籍还到图书馆。
pop()：从图书馆中借出书籍。
为了保持图书的顺序，图书管理员每次取出供读者借阅的书籍是 最早 归还到图书馆的书籍。你需要返回 每次读者借出书的值 。

如果没有归还的书可以取出，返回 -1 。

示例 1：

输入：
[“BookQueue”, “push”, “push”, “pop”]
[[], [1], [2], []]
输出：[null,null,null,1]
解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.pop(); // return 1, queue is [2]

==简单的队列操作==

import java.util.*;
class CQueue {

    Queue<Integer> queue;
    public CQueue() {
        queue = new LinkedList<Integer>();
    }
    
    public void appendTail(int value) {
        queue.offer(value);
    }
    
    public int deleteHead() {
        if(!queue.isEmpty()){
            int res = queue.peek();
            queue.poll();
            return res;
        }else{
            return -1;
        }
        
    }
}

/**
 * Your CQueue object will be instantiated and called as such:
 * CQueue obj = new CQueue();
 * obj.appendTail(value);
 * int param_2 = obj.deleteHead();
 */

最小栈

请你设计一个 最小栈 。它提供 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

• MinStack() 初始化堆栈对象。

• void push(int val) 将元素val推入堆栈。

• void pop() 删除堆栈顶部的元素。

• int top() 获取堆栈顶部的元素。

• int getMin() 获取堆栈中的最小元素。

==采用两个栈，其中一个存储所有的数字，另一个按照越向栈顶数字越小的方式形成==

因为在栈中，对于栈上部的操作是不会影响下面的数字的

class MinStack {
    public Stack<Integer> s1;
    public Stack<Integer> s2;
    /** initialize your data structure here. */
    public MinStack() {
        s1 = new Stack<Integer>();
        s2 = new Stack<Integer>();

    }
    
    public void push(int x) {
        s1.push(x);
        if(s2.empty() || s2.peek() >= x){
            s2.push(x);
        }
    }
    
    public void pop() {
        if(s1.peek().equals(s2.peek())){
            s2.pop();
        }
        s1.pop();
    }
    
    public int top() {
        return s1.peek();
    }
    
    public int getMin() {
        return s2.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

验证图书取出顺序

现在图书馆有一堆图书需要放入书架，并且图书馆的书架是一种特殊的数据结构，只能按照 一定 的顺序 放入 和 拿取 书籍。

给定一个表示图书放入顺序的整数序列 putIn，请判断序列 takeOut 是否为按照正确的顺序拿取书籍的操作序列。你可以假设放入书架的所有书籍编号都不相同。

==直接模拟栈即可==

class Solution {
    public boolean validateBookSequences(int[] putIn, int[] takeOut) {
        Stack<Integer> stack = new Stack<Integer>();
        int index = 0;
        for(int i = 0; i < takeOut.length; i++){
            if(stack.empty()){
                if(index != putIn.length){
                    stack.push(putIn[index++]);
                }else {return false;}
            }
            if(stack.peek().equals(takeOut[i])){
                stack.pop();
            }else{
                if(index != putIn.length){
                    stack.push(putIn[index++]);
                }else return 1 == 0;
                i--;
            }
        }
        return true;
    }
}

望远镜中最高海拔

科技馆内有一台虚拟观景望远镜，它可以用来观测特定纬度地区的地形情况。该纬度的海拔数据记于数组 heights ，其中 heights[i] 表示对应位置的海拔高度。请找出并返回望远镜视野范围 limit 内，可以观测到的最高海拔值。

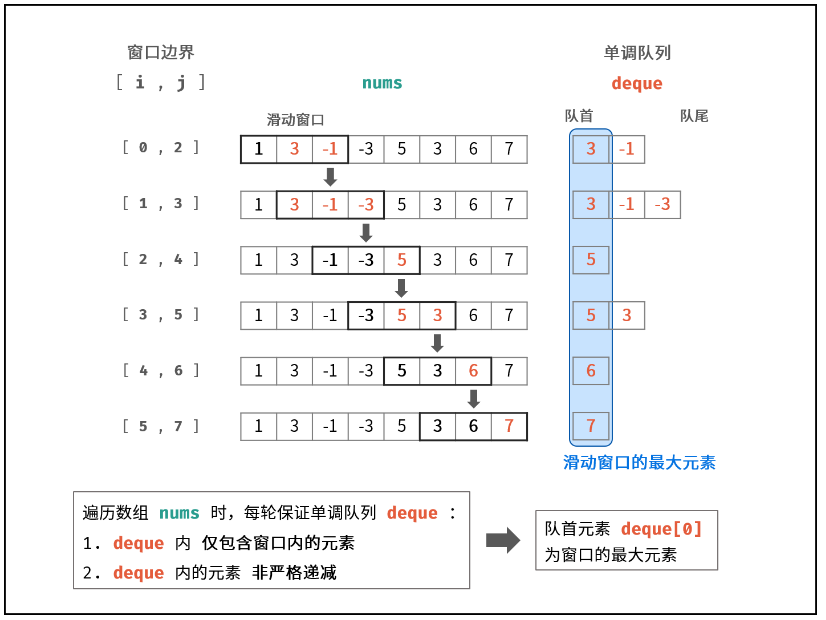
单调队列内每次仅仅有队首（所需要的最大值），队列后所存储的是以后可能作为最大值出现的值。维护这个单调队列即可。

import java.util.ArrayDeque;
import java.util.Deque;

class Solution {
    public int[] maxAltitude(int[] heights, int limit) {

        Deque<Integer> d = new ArrayDeque<>();
        int heightLen = heights.length;
        if(heightLen == 0) return new int []{};
        int [] ans = new int[heightLen - limit + 1];
        //滑动窗口形成之前
        for(int i = 0; i < limit; i++){
            while(!d.isEmpty() && heights[i] > d.peekLast()){
                d.removeLast();
            }
            d.addLast(heights[i]);
        }
        ans[0] = d.peekFirst();
        int j = 1;
        //滑动窗口形成之后
        for(int i = limit; i < heightLen; i++){
            //判断是否需要移除已经不在滑动窗口之内的元素
            if(d.peekFirst() == heights[i-limit]) d.removeFirst();
            while(!d.isEmpty() && heights[i] > d.peekLast()){
                d.removeLast();
            }
            d.addLast(heights[i]);
            ans[j++] = d.peekFirst();
        }
        return ans;
    }
}

设计自助结算系统

请设计一个自助结账系统，该系统需要通过一个队列来模拟顾客通过购物车的结算过程，需要实现的功能有：

• get_max()：获取结算商品中的最高价格，如果队列为空，则返回 -1

• add(value)：将价格为 value 的商品加入待结算商品队列的尾部

• remove()：移除第一个待结算的商品价格，如果队列为空，则返回 -1

注意，为保证该系统运转高效性，以上函数的均摊时间复杂度均为 O(1)

==与上一题有异曲同工之妙，不过这里并没有窗口大小的限制，改成了出队的调用时间控制窗口==

import java.util.ArrayDeque;
import java.util.Deque;
import java.util.LinkedList;
import java.util.Queue;

class Checkout {
    public Deque<Integer> d = new ArrayDeque<>();
    public Queue<Integer> q = new LinkedList<>();

    public Checkout() {

    }

    public int get_max() {
        if(d.isEmpty()) return -1;
        return d.peekFirst();
    }

    public void add(int value) {
        q.add(value);
        while(!d.isEmpty() && value > d.peekLast()){
            d.removeLast();
        }
        d.addLast(value);
    }

    public int remove() {
        if(q.isEmpty()) return -1;
        int res = q.peek();
        q.remove();
        if(res == d.peekFirst()){
            d.removeFirst();
        }
        return res;
    }
}

/**
 * Your Checkout object will be instantiated and called as such:
 * Checkout obj = new Checkout();
 * int param_1 = obj.get_max();
 * obj.add(value);
 * int param_3 = obj.remove();
 */

数据流中的中位数

中位数 是有序整数列表中的中间值。如果列表的大小是偶数，则没有中间值，中位数是两个中间值的平均值。

例如，
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构：

• void addNum(int num) - 从数据流中添加一个整数到数据结构中。

• double findMedian() - 返回目前所有元素的中位数。

==大根堆与小根堆==

import java.util.PriorityQueue;

class MedianFinder {
    //小根堆，这里存储大的数字
    PriorityQueue<Integer> p1 = new PriorityQueue<>((x, y) -> (x - y));
    //大根堆，这里存储小的数字
    PriorityQueue<Integer> p2 = new PriorityQueue<>((x, y) -> (y - x));
    /** initialize your data structure here. */
    public MedianFinder() {

    }

    public void addNum(int num) {
        if(p1.size() == p2.size()){
            p2.add(num);
            p1.add(p2.poll());
        }
        else{
            p1.add(num);
            p2.add(p1.poll());
        }
    }

    public double findMedian() {
        if(p1.size() == p2.size()){
            return (double)(p1.peek() + p2.peek()) / 2.0;
        }else{
            return p1.peek();
        }
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */